KMP(Knuth-Morris-Pratt)算法是一种高效的字符串匹配算法,用于在一个主串中查找一个模式串的位置。它通过预处理模式串,避免了在匹配失败时重复比较已经匹配的部分,从而提高了匹配效率。
该算法在1977年被提出,取三位贡献者的姓名首字母组成算法名称。
什么是字符串匹配
字符串匹配问题是计算机科学中的一个经典问题,其核心目标是在一个较长的文本串(Text)中查找是否存在一个或多个与给定模式串(Pattern)完全相同的子串。
例如:
- 文本串(T):
"ABABDABACDABABCABAB" - 模式串(P):
"ABABCABAB"
那么模式串可以在文本串的索引11处匹配
暴力解法
知道控制语句用法的人都知道,这个问题可以套两层循环来解决,从文本串的第1个字符开始,与模式串逐字符比对,如果发现不匹配,则从文本串的第2个字符开始重新比对,以此类推,该解法时间复杂度为$O(m*n)$,效率较低。
KMP算法
KMP算法通过预处理模式串,利用已经匹配的信息,减少重复比较,将时间复杂度优化至$O(m+n)$
其核心思想有两点:
- 构造模式串的部分匹配表,也叫做前缀表,这个表记录了模式串的最长公共前后缀的长度
- 利用失败信息,当字符不匹配时,根据部分匹配表移动模式串指针的位置,而不需要回溯文本串的位置
下图可以清晰地看出前缀表的含义:

具体实现
构造模式串的部分匹配表,即前缀表:
void getprefix(const string &s, int *prefix){
int fend = 0;
prefix[0] = 0;
for (int bend = 1; bend < s.size(); bend++){
while (fend > 0 && s[fend] != s[bend]){
fend = prefix[fend - 1];
}
if (s[bend] == s[fend]) fend++;
prefix[bend] = fend;
}
}这其中有一些类似递归的思想,当我们手动实现前缀表时,当遇到前缀最后一个字符与后缀字符不匹配的情况时,我们只需要去找他前一位的前缀表的值所指引的位置,从那个位置再次开始对比。
道理和字符串匹配中的应用是一样的,因为前一位存放的是在当前字符之前的子串最大相等前后缀的长度,索引之后代表你可以跳过对比几个前后缀都有的字符,提高效率。
在具体字符串匹配问题中,运用也是一个道理:
int strStr(string haystack, string needle) {
if (needle.size() == 0) return 0;
if (needle.size() > haystack.size()) return -1;
vector<int> prefix(needle.size());
getprefix(needle, &prefix[0]);
int index = 0;
for (int i = 0; i < haystack.size() ; i++){
while (index > 0 && haystack[i] != needle[index]) {
index = prefix[index - 1];
}
if (haystack[i] == needle[index]) index++;
if (index == needle.size()) return (i - index + 1);
}
return -1;
}
补充:
由这个经典问题可推出:一个字符串是否由某个子串重复构成问题的解法。
结论是,如果一个字符串在去掉其最长相等前后缀的长度后,剩余的子串长度能被原始长度整除,那么原始字符串就能被这个剩余的子串重复表示。
充分性证明,即如果某字符串去掉最长相等前后缀后的剩余子串长度能整除原始长度,则原始字符串可由该剩余子串重复表示。
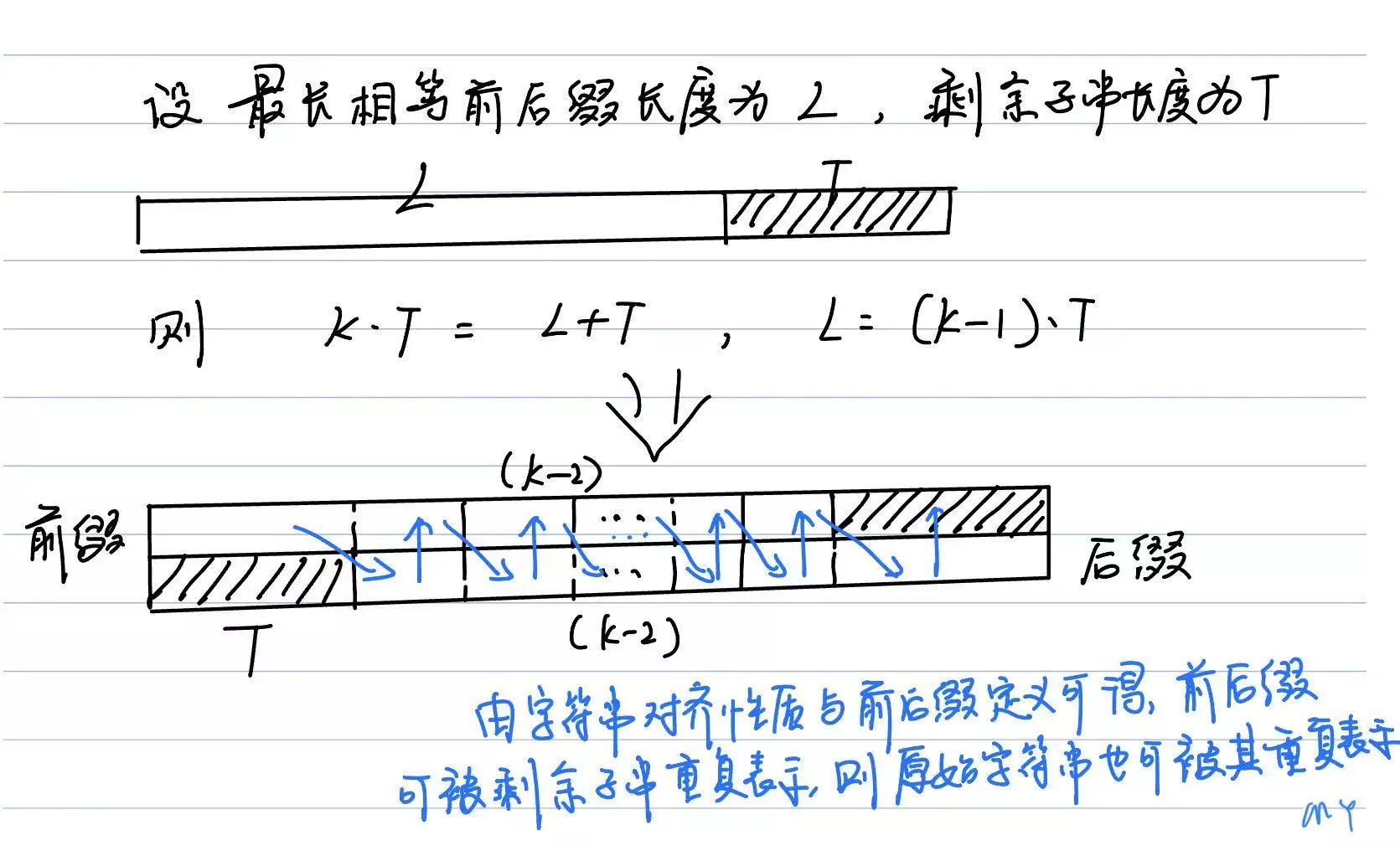
必要性证明,即如果字符串能被某个子串重复表示,则去掉字符串的最长相等前后缀后的剩余子串长度必能整除原始长度。
必要性显然,因此充分必要性均满足,证毕。